1.背景

    20世纪90年代，意大利学者M.Dorigo,V.Maniezzo,A.Colorni等从生物进化的机制中受到启发，通过穆尼自然界蚂蚁搜索路径的行为，提出来一种新型的模拟进化算法——蚁群算法，在1991年ECAL上发表“Distributed optimization by ant colonies”，在其提出之后近五年中并没有在国际学术界引起广泛的关注。1996年，Dorigo M等在《IEEE Transaction on Systems，Man，and Cybernetics-Part B》上发表了“Ant system:optimization by a colony of cooperating agents”一文，在这篇文章中，Dorigo M不仅更加系统地阐述了蚁群算法的基本原理和数学模型，还将其与遗传算法、禁忌搜索算法、模拟退火算法、爬山法等等进行了仿真实验比较，并把单纯地解决对称TSP拓展到解决非对称TSP、指派问题（Quadratic scheduling problem，QAP）以及车间作业调度问题（job-shop scheduling problem,JSP）,并且对蚁群算法中初始化参数对其性能影响做了初步的探讨，这是蚁群算法发展史上的又一篇奠定性文章。虽然研究时间不长，但是现在的研究显示出，蚁群算法在求解复杂优化问题上，尤其是离散优化问题上有一定的优势，表明它是有一种发展前景的算法。这种方法能够被用作解决大多数优化问题或者能够转化为优化求解的问题。现在起应用领域已经扩展到多目标优化、数据分类、数据聚类、模式识别、电信管理、生物系统建模，流程规划、信号处理、机器人控制、决策支持以及仿真和系统辨识等方面，群智能理论和方法为解决这类应用问题提供了新的途径。

2.蚁群算法简介

    群智能理论研究领域有两种主要的算法：蚁群算法(Ant Colony Optimization, ACO)和微粒群算法（Particle Swarm Optimization, PSO）。前者是对蚂蚁群落食物采集过程的模拟，已成功应用于许多离散优化问题。微粒群算法也是起源于对简单社会系统的模拟，最初是模拟鸟群觅食的过程，但后来发现它是一种很好的优化工具。与大多数基于梯度的应用优化算法不同，群智能依靠的是概率搜索算法。这种概率搜索算法与传统梯度下降算法还是有些显著的优势，主要表现为以下方面：

1) 无集中控制约束，不会因个别个体的故障影响整个问题的求解，确保了系统具备更强的鲁棒性;

2) 以非直接的信息交流方式确保了系统的扩展性;

3) 对问题定义的连续性无特殊要求

4) 算法的实现相对较为简单

    最初提出的AS有三种版本：Ant-density、Ant-quantity和Ant-cycle。在Ant-density和Ant-quantity中蚂蚁在两个位置节点间每移动一次后即更新信息素，而在Ant-cycle中当所有的蚂蚁都完成了自己的行程后才对信息素进行更新，而且每个蚂蚁所释放的信息素被表达为反映相应行程质量的函数。通过与其它各种通用的启发式算法相比，在不大于75城市的TSP中，这三种基本算法的求解能力还是比较理想的，但是当问题规模扩展时，AS的解题能力大幅度下降。

故而在其后ACO研究工作主要都集中于AS性能的改进方面中。

策略一：精英算法

    这种思想是在算法的开始后即对所有已知发现的最好路径给予额外的增强，并将随后与之对应的行程记为$T^{gb}$(全局最优行程)，当信息素更新时刻，对这些行程予以加权处理，同时将经过这些行程的蚂蚁记为“精英”，从而取得较好行程选择机会。所以这种算法可以在一定程度上获得更好的解。但是如果是选择过多的精英则算法会由于较早收敛于局部解从而导致搜索的过早停滞。

策略二：信息素增强模式

    为了进一步客服AS中暴露出的问题，提出了蚁群系统(Ant Colony System，ACS)。该系统的提出是以Ant-Q算法为基础的。Ant-Q将蚂蚁算法和一种增强型学习算法Q-learning有机地结合了起来。ACS与AS之间存在三方面的主要差异：首先，ACS采用了行为选择规则；其次，只增强术语全局最优解的路径上的信息素。其中，$0<\rho<1$是信息素挥发参数，$L^{gb}$是从寻路开始到当前为止全局最优的路径长度。信息素更新公式如下表示：

其中$\Delta\tau_{ij}^{gb}(t)=\frac{1}{L^{gb}}$.

    再次，还引入了负反馈机制，每当一只蚂蚁由一个节点移动到另一个节点时，该路径上的信息素都按照如下公式被相应的消除一部分，从而实现一种信息素的局部调整，以减小已选择过的路径再次被选择的概率:

其中$0<\xi<1$.

策略三：Rank-based Version AS

    与“精英策略”相似，在此算法中总是更新更好进程上的信息素，选择的标准是其行程长度$L^{1}(t)\leq L^{2}(t)\leq … \leq L^{m}(t)$决定的排序，且每个蚂蚁释放信息的强度通过以下公式中的排序加权处理确定，其中$w$为每次迭代后放置信息素的蚂蚁总数:

其中$\Delta\tau_{ij}^{r}(t)=\frac{1}{L^{r}}$，$\Delta\tau_{ij}^{gb}(t)=\frac{1}{L^{gb}}$

    这种算法求解TSP的能力与AS、精英策略AS、遗传算法GA和模拟退火算法进行了比较。在大型TSP问题中（最多包含132座城市），基于AS的算法都显示出了优于GA和SA的特性。而且在Rank-based AS和精英策略AS均优于基本AS的同时，前者还获得了比精英策略AS更好的解。

3.蚁群算法与TSP问题求解

    TSP问题描述如下：

    一个N个城市的有向图$G=(N,A)$,其中$N={1,2,…,N}$，$A={(i,j)|i,j\in N}$,城市之间的距离为一个$N\times N$的矩阵$(d_{ij})_{n\times{n}}$,目标函数为$f(w)=\sum_{l=1}^{n}d_{i_{l-1}i_{l}}$ 其中$w$为城市$1,2,…,n$的一个排列$w=(i_{1},i_{2},…,i_{n})$，$i_{n+1}=i_{1}$ TSP问题的蚁群算法中，假设$m$只蚂蚁在图中的相邻节点间移动，从而协作异步地得到问题的解。每只蚂蚁的一步转移概率由图中的每一条边上的两类参数决定：

1) 信息素值，也叫作信息素痕迹

2) 可见度，即先验值

    信息素的更新方式有两种方法，一种是挥发，即路径上的信息素以一定的比率进行减少，模拟自然蚁群的信息素随时间挥发的过程；二是增强，给评价“好”（由蚂蚁走过）的变增加信息素。蚂蚁的下一步目标运动点是通过一个随机原则来实现的，也就是运用当前所在节点存储的信息，计算出下一步可以达到节点的概率，并按此概率实现一步移动，逐此往复，这样会越来越接近最优解。蚂蚁在寻找过程中，或者找到一个解之后，会评估该解或解的一部分的优化程度，并把评价信息保存在相关连接的信息素中。

4. 算法模型的建立

4.1 数学模型

    对于TSP问题，为了不失去一般性，设整个蚂蚁群体中蚂蚁的数量为$m$，城市的数量为$n$，城市$i$与$j$之间的距离为$d_{ij},(i,j=1,2,…,n)$，$t$时刻城市$i$与城市$j$连接路径上的信息素浓度为$\tau_{ij}(t)$。在初始的时刻，蚂蚁分布于不同的城市中，且各城市间连接路径上的信息素浓度相同，不妨假设$\tau_{ij}(0)=\tau_{0}$。然后蚂蚁将按照一定概率选择路线，不妨设概率的大小为$p_{ij}^{k}(t)$为$t$时刻蚂蚁$k$从城市$i$转移到城市$j$的概率。一般定义

    其中，$\eta_{ij}(t)$为启发函数，表示蚂蚁从城市$i$转移到城市$j$的期望程度；$\text{allow}_{k},(k=1,2,…,m)$为蚂蚁$k$待访问的城市集合，开始的时候$\text{allow}_{k}$中有$n-1$个元素，即包括除了蚂蚁$k$出发城市的其他很多城市，随着算法过程中时间推移$\text{allow}_{k}$元素越来越少，直到为空；$\alpha$是信息素重要程度因子(信息素因子)，值越大表示信息素影响越大；$\beta$为启发函数重要程度因子(启发函数因子)，值越大表明启发函数影响影响越大。

    蚂蚁遍历每一个城市过程中，蚂蚁释放信息素的时候，各个城市之间连接路径上信息素强度也在通过挥发的方式逐渐消失。设信息素挥发程度因子为$\rho$，所以当所有蚂蚁完整遍历过一遍所有城市之后，各个城市之间连接的信息素浓度为

    其中，$\Delta\tau_{ij}^{k}$是第$k$只蚂蚁在城市$i$与城市$j$连接路径上释放的信息素的增加量。 其中启发函数定义为：

$d_{ij}$表示城市之间的距离矩阵。     在Ant cycle system 模型中，$\Delta\tau_{ij}^{k}$一般定义为

    其中，$Q$为信息素常数，表示蚂蚁循环一次所释放的信息素总量；$L_{k}$是第$k$只蚂蚁经过路径的总长度。在其他的蚁群算法系统中，在TSP问题上对$\Delta\tau_{ij}^{k}$的计算不尽相同。还有两种基本的蚁群算法，即Ant quantity system模型和Ant density system模型。 在 Ant quantity system中，$\Delta\tau_{ij}^{k}$一般定义为： $\Delta\tau_{ij}^{k}$一般定义为

$d_{ij}$是城市$i$和城市$j$之间距离。在Ant density system模型中，$\Delta\tau_{ij}^{k}$一般定义为：

    常数$Q$表示蚂蚁一次循环所释放信息素总量。这三种方法主要的区别是，Ant cycle system使用的是整体的信息，后面两种是局部信息，相对来说Ant cycle system在处理TSP问题过程中具有较好的性能，通常作为基本的蚁群模型。

4.2 算法流程

步骤1：对蚁群算法中的相关参数进行初始化处理。参数信息包括有：蚁群的规模($m$)、信息素因子($\alpha$)、启发函数因子($\beta$)、信息素挥发因子($\rho$)、信息素常数($Q$)、最大迭代次数($\text{epoches})$等等参数信息，另外还包括有程序读入的数据信息。

步骤2：随机将蚂蚁放置于不同出发点，对每一个蚂蚁计算其下一个访问的城市，直到访问完毕所有的城市。

步骤3：计算每个蚂蚁经过的路径长度$L_{k}$，记录当前迭代次数中的最优解，同时更新各个城市连接路径上的信息素浓度。

步骤4；是否达到迭代次数上限，若是则结束程序，如若否，则返回步骤2，继续求解。

5. 算法具体应用

5.1 TSP问题的求解

    数据的准备：我们在这里选取TSP问题数据集TSP问题数据集。在本文中我们选取数据集eil51.tsp进行问题的求解。

在蚂蚁选择下一个城市访问的方法中，我们使用到了轮盘赌算法，它的基本过程如下所示： (1) 计算每个个体的适应度比例，即每个个体的选择概率

(2) 计算每个个体的累积概率，相当于在轮盘中的跨度，跨度越大则被选中的概率越大：

也就是每个个体之前所有个体的选择概率之和，相当于概率论中的概率分布函数$F(x)$ (3) 随机生成$r\in{[0,1]}$，若$q_{i}>r$，则选择个体$x_{i}$。

程序运行之后的结果信息如下所示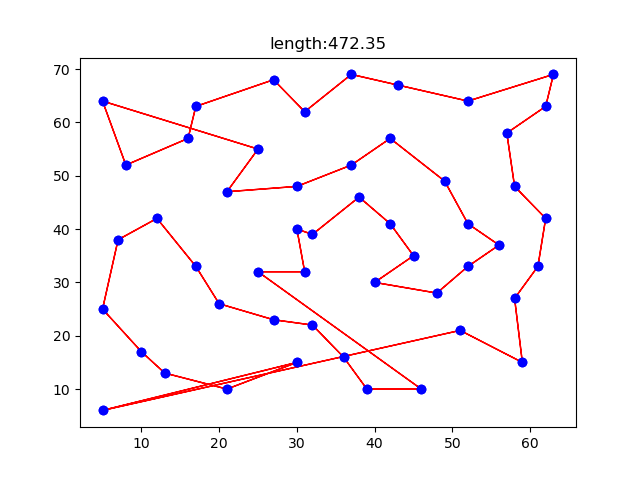： 每次迭代过程中平均路径长度的变化如下所示：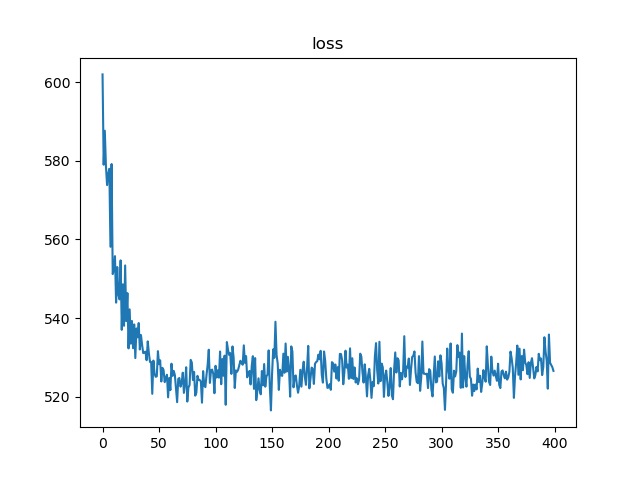

    由平均路径长度的变化图可知，蚁群算法是趋近于收敛的。程序的结果虽然并不是很好，经过多次训练之后程序结果可能会更佳。笔者将蚁群算法用python版本和MATLAB版本进行的实现，具体代码可以查找笔者GitHub。

5.2 参数的选择

    一般来说，参数的选择遵循以下的原则：

(1) 尽可能在全局上搜索最优解，用以保证解的最优性质；

(2) 算法尽快收敛，节约寻优的时间；

(3) 尽量反应出客观的存在规律，以保证这种仿生算法的真实性。

    蚂蚁数量的选择：蚂蚁数量取决于问题规模的大小形式。一般来说，城市的数量$M$和蚂蚁的数量$m$应该适当均衡，参数$m$太大，会使得被搜索过的路径上的信息素变化趋近于平均，正反馈作用减弱，以导致收敛速度减慢；反之，处理较大问题时候，容易使得未被搜索到的路径信息素量减小到$0$，使得程序过早出现停滞现象，从而使得全局优化型降低。

    信息素因子：它反映出了蚂蚁在运动过程中所积累的信息量在指导蚂蚁群搜索中的相对重要程度，它的值越大，那么在之前走过的路径可能性就会越大，搜索的随机性减弱；其值过小，则等同于贪婪算法，容易陷入局部最优情况。一般情况下选择$\alpha\in{[1,4]}$。

    启发函数因子：启发函数因子$\beta$，反应出的是启发式信息在指导蚁群算法过程中的重要程度，它的值反映了蚁群寻优过程中的先验性、确定性因素作用的强度。一般来说选择$\beta\in{[3,4.5]}$。

    信息素挥发因子：反映出信息素挥发消失的水平，$(1-\rho)$表达的是信息素残留因子，描述信息素保持的水平大小。一般情况下选择$\rho\in{[0.2,0.5]}$。

    信息素常量：常数$Q$是信息素常量，表示的是蚂蚁在循环一周的时候释放在路径上的信息素总量。一般选取$Q\in{[10,1000]}$。

6. 小结

    本小结详细讲述了蚁群算法在TSP问题中的具体应用。需要注意的是，蚁群算法在不同方面的应用和使用，以保证蚁群算法的实用性和可靠性。