MobtgZhang

翻译模型在知识图谱中的应用(二):基于高斯模型

2021/04/22 翻译模型 共 5388 字，约 16 分钟

1. 简介

    在上一次博文中重点讨论了一些用于生成Embedding预训练向量最为基本的模型,例如TransE、TransR、TransH等等很多模型,但是这些模型中存在有多种不确定的影响因素，所以直接以距离模型稍微有些欠缺.因此提出一种基于高斯分布的模型来对Embedding进行预训练.

2. 基于高斯分布模型

2.1 KG2E 模型

    由于上述的几种翻译模型中的方法都是将实体和关系嵌入到点向量空间中,这些模型总是以同样的方式看待所有的实体和关系,由于实体库中的实体和关系本身就存在一定的不确定性,以前的方法模型忽略了这一不确定性因素.

    模型中存在有多种不确定的影响因素:

  • 关系两边的头实体和尾实体的不对称性
  • 不同关系和实体连接的三元组数量的不同
  • 关系的模糊不清

    KG2E不再使用点空间而是采用基于密度的向量嵌入方法,这里使用高斯分布的方法来表示实体和关系,用均值表示其所处的中心位置,用协方差表示实体和关系的不确定度,使用KL散度对三元组进行打分处理.论文中将每个关系和实体使用多维高斯分布$\mathcal{N}(\mu,\Sigma)$表示.

    KG2E模型中使用h-t表示头尾实体之间的关系,可以计算得到概率分布表示:

\[\mathcal{P}_{e}\sim\mathcal{N}(\mu_{h}-\mu_{t},\Sigma_{h}+\Sigma_{t})\]

关系大概率分布可以表示为

\[\mathcal{P}\sim\mathcal{N}(\mu_{r},\Sigma_{r})\]

然后可以评估$\mathcal{P}{e}$和$\mathcal{P}{r}$之间的相似度,论文中提出了两种评分的方式:

(1) 非对称相似度:实体分布和关系分布之间的KL散度:

\[\mathcal{D}_{\mathcal{KL}}(\mathcal{P}_{e},\mathcal{P}_{r})=\int_{x\in{\mathcal{R}^{k_{e}}}}\mathcal{N}(x;\mu_{r},\Sigma_{r})\log\dfrac{\mathcal{N}(x;\mu_{e},\Sigma_{e})}{\mathcal{N}(x;\mu_{r},\Sigma_{r})}dx\] \[=\dfrac{1}{2}\left\{tr(\Sigma_{r}^{-1}\Sigma_{e})+(\mu_{r}-\mu_{e})^{T}\Sigma_{r}^{-1}(\mu_{r}-\mu_{e})-\log\dfrac{\det\Sigma_{e}}{\det\Sigma_{r}}-k_{e}\right\}\]

所以现在定义基于KL散度的对称相似度度量方法:

\[\epsilon(h,r,t)=\epsilon(\mathcal{P}_{e},\mathcal{P}_{r})=\dfrac{1}{2}\left[\mathcal{D}_{\mathcal{KL}}(\mathcal{P}_{e},\mathcal{P}_{r})+\mathcal{D}_{\mathcal{KL}}(\mathcal{P}_{r},\mathcal{P}_{e})\right]\]

备注这个等式推理的方法如下所示:

\[\mathcal{N}(x;\mu_{e},\Sigma_{e})\]

(2) 对称相似度表示(EL):采用期望似然的方法,使用两个分布的内积作为度量两个分布的相似度

\[\epsilon(\mathcal{P}_{e},\mathcal{P}_{r})=\int_{x\in{\mathcal{R}}^{k_{e}}}\mathcal{N}(x;\mu_{e},\Sigma_{e})\mathcal{N}(x;\mu_{r},\Sigma_{r})dx\] \[=\mathcal{N}(0;\mu_{e}-\mu_{r},\Sigma_{e}+\Sigma_{r})\]

使用对数处理:

\[\epsilon(h,r,t)=\log\epsilon(\mathcal{P}_{e},\mathcal{P}_{r})\] \[=\log\epsilon\mathcal{N}(0;\mu_{e}-\mu_{r},\Sigma_{e}+\Sigma_{r})\] \[=\dfrac{1}{2}\left\{(\mu_{e}-\mu_{r})^{T}(\Sigma_{e}+\Sigma_{e})^{-1}(\mu_{e}-\mu_{r})+\log\left[\det\left(\Sigma_{e}+\Sigma_{r}\right)\right]+k_{e}\log(2\pi)\right\}\]

所以这样定义以下的损失函数

\[\mathcal{L}=\sum\limits_{(h,r,t)\in\Gamma,(h^{\prime},r^{\prime},t^{\prime})\in\Gamma^{\prime}}\left[\epsilon(h,r,t)+\gamma-\epsilon(h^{\prime},r^{\prime},t^{\prime})\right]_{+}\]

同时需要满足以下约束:

\[\forall\in{\epsilon\cup\mathcal{R}},\left|\left|\mu_{l}\right|\right|_{2}\leq{1}\] \[\forall\in{\epsilon\cup\mathcal{R}},c_{\min}I\leq{\Sigma_{l}}\leq{c_{\max}I},c_{\min}>0\]

2.2 TransG模型

    TransG模型2也是一种高斯分布的模型,它主要解决的问题是同一种关系在不同的实体对上的语义是不同的.在TransE模型中对关系进行PCA降维可视化处理,其中点的位置代表头尾实体的向量差值$t-h$,从下图中可以看出同一种关系连接不同类型的实体对的时候,其会聚类在不同的簇中,所以这样的问题是确实存在的.

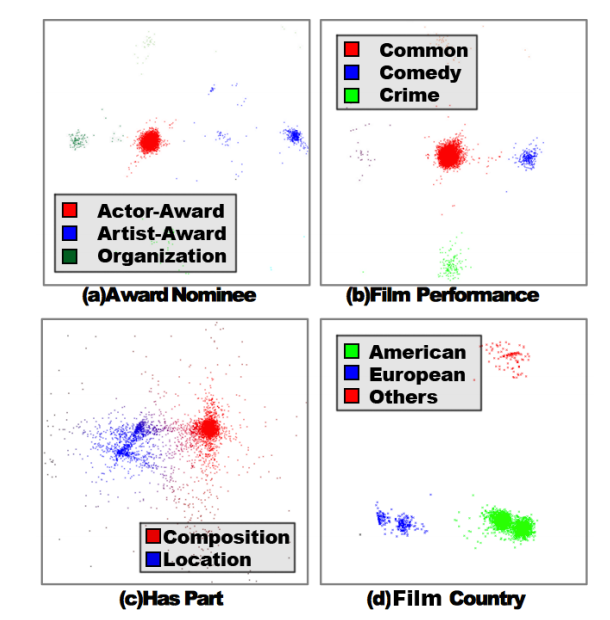
TransG模型中同一种关系不同实体对上语义可视化图

    论文中使用到了贝叶斯非参数高斯混合模型(Bayesuan non-parametric mixture embedding model)对一个关系生成多个翻译部分,它能够自动发现关系的语义簇,根据三元组的特定语义得到当中最佳部分.

模型构造的方法如下所示:

  1. 对于一个实体$e\in{E}$,从正态分布$u_{e}\sim{\mathcal{(0,1)}}$生成每个实体嵌入向量的均值向量.
  2. 对于一个三元组$(h,r,t)\in{\Delta}$:
    • 为该关系生成一个语义分量:$\pi_{r,m}\sim{CRP}(\beta)$.
    • 从正态分布中初始化头实体embedding:$h\sim\mathcal{N}(u_{h},\sigma_{h}^{2}E)$.
    • 从正态分布中初始化尾实体embedding:$t\sim\mathcal{N}(u_{t},\sigma_{t}^{2}E)$.
    • 对该语义初始化关系向量$u_{r,m}=(t-h)\sim{\mathcal{N}(u_{t}-u_{h},(\sigma_{h}^{2}+\sigma_{t}^{2})E)}$.

    其中,$u_{h}$和$u_{t}$分别表示头实体和尾实体的均值向量,$\sigma_{h},\sigma_{t}$分别表示头实体和尾实体分布的方差,$u_{r,m}$表示关系$r$第$m$个子关系向量.$CRP$是一个狄利克雷过程,能够自动检测语义分量.

定义得分函数

\[\mathbb{P}\left\{(h,r,t)\right\}\propto\sum\limits_{m=1}^{M_{r}}\pi_{r,m}\mathbb{P}(u_{r,m}|h,t)=\sum\limits_{m=1}^{M_{r}}\pi_{r,m}e^{-\frac{\left|\left|u_{h}+u_{r,m}-u_{t}\right|\right|_{2}^{2}}{\sigma_{h}^{2}+\sigma_{t}^{2}}}\]

其中,$\pi_{r,m}$是混合因子,表示关系$r$中第$i$个分量的权重,$M_{r}$是关系$r$的子语义个数,通过CRP自动从数据中学习得到.

    注意,这里有一个最为重要的问题就是一种狄利克雷分布的问题,最为典型的一个模型就是CRP过程的模型,

Chinese Restaurant Process(CRP) 中国餐馆过程是一个典型的Dirichlet过程混合模型,模型描述如下所示:

(1) 有一个中国餐馆,可以由无限张桌子,每次只能有且仅有一张空桌子,如果空桌子有人选择坐下,那么新增一个空桌子.

(2) 来吃饭的第一位顾客坐了第一张桌子.

(3) 对于每一位顾客,按照以下的规则选择桌子坐下,对于第n个顾客:

  • 顾客选择已经有人的第k张桌子的概率为$\dfrac{n_{k}}{\alpha_{0}+n-1}$.其中,$n_{k}$表示第$k$张桌子已经有的顾客数量,$n-1$表示在这个顾客之前,餐馆已经有的顾客数量.
  • 顾客选择没有人坐的桌子上$K+1$的概率为$\dfrac{\alpha_{0}}{\alpha_{0}+n-1}$.

论文中也给出了对应的几何化解释TransG模型,TransG是上述表达式的一般化的形式:

\[m_{(h,r,t)^{*}}=\underset{m=1,\dots,M}{\arg\max}\left(\pi_{r,m}e^{-\left|\left|h+u_{r,m}-t\right|\right|_{2}^{2}}\right)\] \[h+u_{r,m_{(h,r,t)}^{*}}\approx{t}\]

训练方法 采用最大化似然原则,对于非参数部分,$\pi_{r,m}$从CRP中得到,对于一个三元组,一个新的子关系从以下概率可以得到:

\[\mathbb{P}(m_{r},\text{new})=\dfrac{\beta{e^{-\frac{\left|\left|h-t\right|\right|_{2}^{2}}{\sigma_{h}^{2}+\sigma_{t}^{2}+2}}}}{\beta{e^{-\frac{\left|\left|h-t\right|\right|_{2}^{2}}{\sigma_{h}^{2}+\sigma_{t}^{2}+2}}}+\mathbb{P}(h,r,t)}\]

其中,\(\mathbb{P}\left\{(h,r,t)\right\}\)是当前的后验概率.损失函数的定义如下所示:

\[\mathcal{L}=-\sum\limits_{(h,r,t)\in{\Delta}}\ln\left(\sum\limits_{m=1}^{M_{r}}\pi_{r,m}{e^{-\frac{\left|\left|u_{h}+u_{r,m}-u_{t}\right|\right|_{2}^{2}}{\sigma_{h}^{2}+\sigma_{t}^{2}}}}\right)\] \[+\sum\limits_{(h^{\prime},r^{\prime},t^{\prime})\in{\Delta}}\ln\left(\sum\limits_{m=1}^{M_{r}}\pi_{r^{\prime},m}{e^{-\frac{\left|\left|u_{h^{\prime}}+u_{r^{\prime},m}-u_{t^{\prime}}\right|\right|_{2}^{2}}{\sigma_{h^{\prime}}^{2}+\sigma_{t^{\prime}}^{2}}}}\right)\] \[+C\left(\sum\limits_{r\in{R}}\sum\limits_{m=1}^{M_{r}}\left|\left|u_{r,m}\right|\right|_{2}^{2}+\sum\limits_{e\in{E}}\left|\left|u_{e}\right|\right|_{2}^{2}\right)\]

    特别地,在训练过程中,方差因子$\pi$以及$\sigma$均会进行训练.

3. 小结

    实际上这类研究开辟了另一种解决预训练向量的问题,即通过一些常见的分布函数生成对应的向量,以增加模型中的不确定度;使用概率的方法对Embedding存在的一些问题进行概率化求解.

参考文献

[1] KG2E模型: He S , Kang L , Ji G , et al. Learning to Represent Knowledge Graphs with Gaussian Embedding[C]// Acm International. ACM, 2015.

[2] TransG模型: Han X , Huang M , Yu H , et al. TransG : A Generative Mixture Model for Knowledge Graph Embedding. computer science, 2015.

文档信息

Search

    Table of Contents