MobtgZhang

常见的论文中模型评价指标

2021/05/01 评价方法 共 2519 字，约 8 分钟

综述

    深度学习以及机器学习中常用到的几种模型评价方法有以下的几种:混淆矩阵中几种方法(ACC,Recall等等)、MRR、Hit@K、NDC等几种方法

混淆矩阵

    混淆矩阵是最为常见的一种模型评价的方法,它是表示精度评价的一种标准格式,用n行n列的矩阵形式来表示.它是一种精度评价的可视化工具,特别是用于监督学习,在无监督学习中一般叫做匹配矩阵.在评价过程中主要用于比较分类结果和实际测得值,可以把分类结果的精度现实在一个混淆矩阵里面.具体以二分类表示如下图所示:

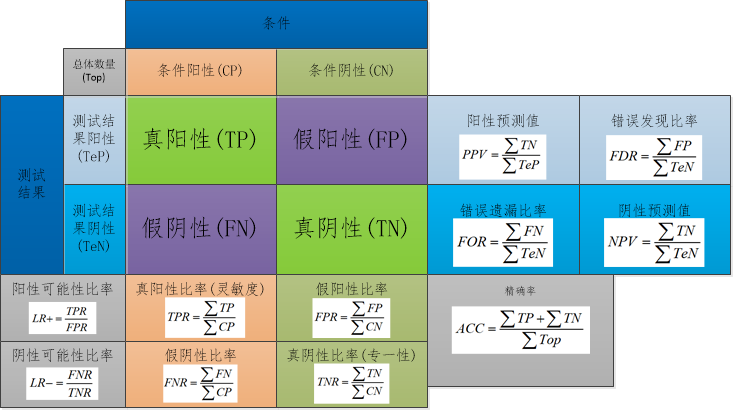
混淆矩阵表示图

    上述图中列举了几个测试的指标,有对应的公式,最常见的公式指的是精确率(ACC).关于混淆矩阵有关的参数如下所示:

  1. 准确率:准确率表示预测正确的样本数量占总样本数量的比例.
\[Acc=\dfrac{TP+TN}{TP+TN+FP+FN}\]
  1. 精确率:精确率表示预测为正样本的样本中,正确预测为正样本的概率.
\[Precision=\dfrac{TP}{TP+FP}\]
  1. 召回率:召回率表示正确预测出正样本占实际正样本的概率
\[Recall=\dfrac{TP}{TP+FP}\]
  1. $F\beta-$score值:这个值类似于召回率,一般情况取$\beta=1$,称为F1-Score值.
\[F_{\beta}=(1+\beta^{2})\cdot\dfrac{Precision\cdot{Recall}}{(\beta^{2}\cdot{Precision})+Recall}\]
  1. ROC曲线与AUC

    ROC曲线的横轴为假正例率FPR(越小越好),纵轴TPR(越大越好).

    AUC值的定义:AUC值为ROC曲线所覆盖的区域面积,显然AUC越大表示分类器分类效果是越好的.评价如下所示:

  • $AUC=1$,表示完美分类器,采用这个预测模型时候,不管设定什么阈值都能得出完美预测.绝大多数预测的场合不存在完美分类器.
  • $0.5<AUC<1$,优于随机猜测,这个模型妥善设定阈值的话,能有预测价值.
  • $AUC=0.5$,这个和随机猜想一样没有预测价值.
  • $0<AUC<0.5$,比随机猜测还差;但只要总是反预测而行,就优于随机猜测.

Hit Ratio(HR)

    HR是一种常用的衡量召回率的指标,计算公式如下所示

\[HR@K=\dfrac{Num@K}{GT}\]

    其中分母GT是所有的测试集合,分子表示每个用户Top-K列表中属于测试集合的个数总和.

Mean Average Precision(MAP)

    平均准确率AP一般使用的以下的情形,举个例子,如果使用某一搜索引擎搜索一个特定关键词返回了10个结果,最好的情况是这10个结果都是想要的相关信息.但是假如只有部分是相关的,例如有5个,那么这5个结果被显示比较靠前的话也是不错的结果,如果是在第6个返回结果才开始出现的话,那么这种情况便是比较差一点的情况.这就是AP所反映的指标,也与召回率是类似的,但是是顺序敏感型的recall.

    对于用户u,给他推荐一些物品,那么u的平均准确率为

\[AP_{u}=\dfrac{1}{\Omega_{u}}\sum\limits_{i\in{\Omega_{u}}}\dfrac{\sum\limits_{j\in{\Omega_{u}}}h(p_{uj}<p_{ui})+1}{p_{ui}}\]

    其中,$\Omega_{u}$表示Ground-Truth的结果,$p_{uj}$表示$i$物品在推荐列表中的位置,$p_{uj}<p_{ui}$表示$j$物品在推荐列表中排在$i$物品之前.

    MAP表示所有用户$u$的AP再取均值,计算公式如下所示:

\[MAP=\dfrac{\sum\limits_{u\in{U}}AP_{u}}{|U|}\]

Normalized Discounted Cummulative Gain(NDCG)

    积累增益CG,在推荐系统中CG表示将每个推荐结果相关性的分值累加之后作为整个推荐列表的得分:

\[CG_{k}=\sum\limits_{i=1}^{k}rel_{i}\]

其中,$rel_{i}$表示位置$i$的推荐结果的相关性,$k$表示推荐列表的大小.

    CG没有考虑每个推荐结果处于不同率位置对整个推荐结果的影响,我们总希望相关性大的结果排在前面,相关性低的排在前面会影响用户体验.

    DCG在CG的基础上引入了位置影响因素,计算公式如下所示:

\[DCG_{k}=\sum\limits_{i=1}^{k}\dfrac{2^{rel_{i}}-1}{\log_{2}(i+1)}\]

    表达式中表明:推荐结果的相关性越大,DCG越大;相关性好的排在推荐列表前面的话,推荐效果越好,DCG越大.

    DCG针对不同的推荐列表之间很难进行横向评估,而我们评估一个推荐系统不可能仅仅使用一个用户的推荐列表及相应结果进行评估,而是对整个测试集中的用户以及其推荐列表结果进行评估.那么不同用户的推荐列表的评估分数就需要进行归一化,也就是NDCG.

    IDCG表示推荐系统某一用户返回的最好推荐结果列表,即假设返回结果按照相关性排序,最相关的结果放在最前面,此序列的DCG为IDCG.因此DCG的值介于$(0,IDCG]\in(0,1]$,那么用户u的NDCG@K定义参数为

\[NDCG_{u}@K=\dfrac{DCG_{u}@K}{IDCG_{u}}\]

平均NDCG的值为

\[NDCG@K=\dfrac{\sum\limits_{u\in{U}}NDCG_{u}@K}{IDCG_{u}}\]

Mean Reciprocal Rank(MRR)

    正确检索结果值在检索结果中的排名来评估检索系统的性能.

\[MRR=\dfrac{1}{Q}\sum\limits_{i=1}^{|Q|}\dfrac{1}{rank_{i}}\]
其中,$Q$是用户的个数,$rank_{i}$是对于第i个用户,推荐列表中第一个在Ground-Truth结果中的item所在的排列位置.

文档信息

Search

    Table of Contents